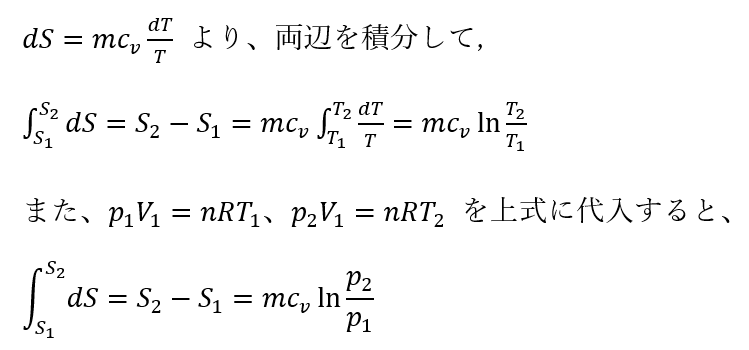微分エントロピー

微分エントロピー（びぶんエントロピー、英: differential entropy）または連続エントロピー（continuous entropy）は情報理論における概念で、シャノン情報量（確率変数が持つ平均的自己情報量の尺度）を連続型確率分布にまで拡張するクロード・シャノンの試みに端を発する。情報量の概念を連続量まで真に拡張したものに limiting density of discrete points（LDDP）がある。本記事で述べる微分エントロピーは文献でよく目にするものだが、LDDPに制限を加えた特別な場合の一つであり、離散的情報量の持つ基本的な性質のいくつかを失っている。

定義

${\displaystyle X}$ を、確率密度関数 ${\displaystyle f}$ の関数の台が ${\displaystyle {\mathcal {X}}}$ である確率変数とする。微分エントロピー ${\displaystyle h(X)}$ または ${\displaystyle h(f)}$ は

と定義される。

明示的な確率密度関数は持っていないが、明示的な分位点関数表示 ${\displaystyle Q(p)}$ を持っている確率変数（確率分布）に対しては ${\displaystyle h(Q)}$ を ${\displaystyle Q(p)}$ の微分として定義できる。つまり、分位点密度関数 ${\displaystyle Q'(p)}$ により

${\displaystyle h(Q)=\int _{0}^{1}\log Q'(p)\,dp}$

と定義する。

離散型の場合と類似して、微分エントロピーの単位は対数の底に依存する（通常は底を2とし、単位はビットとする）。対数の底による違いについては en:logarithmic units を参照。関連した概念である結合、条件付き、相対微分エントロピーも同様に定義される。

離散的な場合とは異なり、微分エントロピーには ${\displaystyle X}$ の計測単位に依存して横ずれが生じる。例えば、ある量をミリメートルで測ったときの微分エントロピーは、同じ量をメートルで測ったときよりも log(1000) だけ大きな値になる。無次元量の微分エントロピーは、その 1/1000 を計量の基本単位として表示したときの微分エントロピーよりも log(1000) だけ大きな値になる。

確率密度関数は1を超える値をとり得るから、離散的なエントロピーの性質を微分エントロピーにも適用するときは注意を要する。例えば、一様分布 ${\displaystyle {\mathcal {U}}(0,1/2)}$ は負の微分エントロピー

${\displaystyle \int _{0}^{\frac {1}{2}}-2\log(2)\,dx=-\log(2)}$

を持つ。

一方で相互情報量 ${\displaystyle I(X;Y)}$ は、連続量に対しても2情報の依存度合の尺度として基本的に重要である。この量は実質的に、離散的な ${\displaystyle X}$ と ${\displaystyle Y}$ にそれぞれ「分割（partition）」を施していき、分割幅を限りなく細かくしていったときの極限に相当するからである。${\displaystyle I(X;Y)}$ は ${\displaystyle X}$ と ${\displaystyle Y}$ を線形な位相同型（自身および逆が連続である写像）で変換しても不変であるばかりでなく非線形同型写像による変換の下でも不変である。相互情報量は、空間的に連続的な値を許すような伝送を介する状況下での2情報量の関係を表現することができる。

離散的なエントロピーが持つ性質の微分エントロピーへの拡張については en:limiting density of discrete points を参照。

微分エントロピーの性質

• 確率密度関数 ${\displaystyle f}$ と ${\displaystyle g}$ に対しカルバック・ライブラー情報量 ${\displaystyle D_{KL}(f||g)}$ は 0 以上であり、0 と一致するのはほとんど至るところで ${\displaystyle f=g}$ であるとき、かつそのときに限る。同様に、2つの確率変数 ${\displaystyle X}$ と ${\displaystyle Y}$ に対し ${\displaystyle I(X;Y)\geq 0}$ かつ ${\displaystyle h(X|Y)\leq h(X)}$ で、等号が成立するのは ${\displaystyle X}$ と ${\displaystyle Y}$ が独立であるとき、かつそのときに限る。
• 離散型の場合と同じく連鎖律が成り立つ。

${\displaystyle h(X_{1},\ldots ,X_{n})=\sum _{i=1}^{n}h(X_{i}|X_{1},\ldots ,X_{i-1})\leq \sum _{i=1}^{n}h(X_{i})}$

• 平行移動不変である。つまり任意の定数 ${\displaystyle c}$ に対し

${\displaystyle h(X c)=h(X)}$

• 一般に、任意の可逆な写像の下で不変ではない。

特に、定数 ${\displaystyle a}$ に対しては

${\displaystyle h(aX)=h(X) \log |a|}$

ベクトル値確率変数 ${\displaystyle \mathbf {X} }$ と可逆な正方行列 ${\displaystyle \mathbf {A} }$ に対しては

${\displaystyle h(\mathbf {A} \mathbf {X} )=h(\mathbf {X} ) \log \left(|\det \mathbf {A} |\right)}$

• 一般に、あるベクトル値確率変数から同じ次元のベクトル値確率変数への変換 ${\displaystyle \mathbf {Y} =m\left(\mathbf {X} \right)}$ があるとき、対応するエントロピーは

${\displaystyle h(\mathbf {Y} )\leq h(\mathbf {X} ) \int f(x)\log \left\vert {\frac {\partial m}{\partial x}}\right\vert dx}$

を満たす。ここで ${\displaystyle \left\vert {\frac {\partial m}{\partial x}}\right\vert }$ は変換 ${\displaystyle m}$ のヤコビ行列式である。この不等式は変換が全単射のとき等式になる。さらに ${\displaystyle m}$ が回転、平行移動、またはそれらの合成であるとき、ヤコビ行列式の値は常に1であり、${\displaystyle h(Y)=h(X)}$ となる。

• 確率変数ベクトル ${\displaystyle X\in \mathbb {R} ^{n}}$ の平均が0で分散共分散行列が ${\displaystyle K}$ のとき

${\displaystyle h(\mathbf {X} )\leq {\frac {1}{2}}\log(\det {2\pi eK})={\frac {1}{2}}\log[(2\pi e)^{n}\det {K}]}$

等号が成立するのは ${\displaystyle X}$ が多変量正規分布に従うとき、かつそのときに限る。

しかし、微分エントロピーは他のいくつかの望ましい性質を持っていない：

• 微分エントロピーは変数変換の下で不変でない。最も有用になるのは変量が無次元の場合である。
• 微分エントロピーは負になり得る。

これらの欠点に対応するため微分エントロピーを修正したものが relative information entropy であり、これは不変測度因子を含んでいる。en:limiting density of discrete points を参照。

正規分布のときに最大になること

定理

平均 ${\displaystyle \mu }$, 分散 ${\displaystyle \sigma ^{2}}$ が固定されたとき、微分エントロピーが最大になるのは分布が正規分布のときである。

証明

${\displaystyle g(x)}$ を平均 ${\displaystyle \mu }$ ・分散 ${\displaystyle \sigma ^{2}}$ の正規分布の確率密度関数とし、${\displaystyle f(x)}$ を同一の平均と分散を持つ任意の確率密度関数とする。

2分布間のカルバック・ライブラー情報量

${\displaystyle 0\leq D_{KL}(f||g)=\int _{-\infty }^{\infty }f(x)\log \left({\frac {f(x)}{g(x)}}\right)dx=-h(f)-\int _{-\infty }^{\infty }f(x)\log(g(x))dx}$

を考える。ここで

${\displaystyle {\begin{aligned}\int _{-\infty }^{\infty }f(x)\log(g(x))dx&=\int _{-\infty }^{\infty }f(x)\log \left({\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\right)dx\\&=\int _{-\infty }^{\infty }f(x)\log {\frac {1}{\sqrt {2\pi \sigma ^{2}}}}dx \log(e)\int _{-\infty }^{\infty }f(x)\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)dx\\&=-{\tfrac {1}{2}}\log(2\pi \sigma ^{2})-\log(e){\frac {\sigma ^{2}}{2\sigma ^{2}}}\\&=-{\tfrac {1}{2}}\left(\log(2\pi \sigma ^{2}) \log(e)\right)\\&=-{\tfrac {1}{2}}\log(2\pi e\sigma ^{2})\\&=-h(g)\end{aligned}}}$

である。よって ${\displaystyle h(g)-h(f)\geq 0\!}$ 。

例：指数分布

${\displaystyle X}$ がパラメータ ${\displaystyle \lambda }$ の指数分布に従う、つまり確率密度関数が

${\displaystyle f(x)=\lambda e^{-\lambda x}{\mbox{ for }}x\geq 0}$

であるとする。この微分エントロピーは

ここで、計算の簡易化のため対数の底を e としていることを明示するため、${\displaystyle h(X)}$ ではなく ${\displaystyle h_{e}(X)}$ と書いている。

推定誤差との関係

微分エントロピーは推定量の平均二乗誤差に対する、一つの下限を与える。任意の連続型確率変数 ${\displaystyle X}$ とその推定統計量 ${\displaystyle {\widehat {X}}}$ に対し、以下が成り立つ：

${\displaystyle \operatorname {E} [(X-{\widehat {X}})^{2}]\geq {\frac {1}{2\pi e}}e^{2h(X)}}$

等号が成立するのは ${\displaystyle X}$ が正規分布に従い、${\displaystyle {\widehat {X}}}$ が ${\displaystyle X}$ の平均であるとき、かつそのときに限る。

様々な分布の微分エントロピー

下記の表で、${\displaystyle \Gamma (x)=\int _{0}^{\infty }e^{-t}t^{x-1}dt}$ はガンマ関数、${\displaystyle \psi (x)={\frac {d}{dx}}\ln \Gamma (x)={\frac {\Gamma '(x)}{\Gamma (x)}}}$ はディガンマ関数、${\displaystyle B(p,q)={\frac {\Gamma (p)\Gamma (q)}{\Gamma (p q)}}}$ はベータ関数、γ_E は オイラーの定数である。

これらの多くについては脚注参照。

関連項目

• 情報量
• 自己情報量
• エントロピー推定

脚注

外部リンク

• Hazewinkel, Michiel, ed. (2001), “Differential entropy”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Differential_entropy 
• Differential entropy - PlanetMath.org（英語）